§ 参考资料 共 6 条
NeRF 中,整个场景用一个函数隐式表示,在渲染时,通过对这个隐式函数积分来求出每一个像素的颜色值,这样的方法被称为 backward mapping
而 3DGS 使用高斯椭球描绘整个场景,渲染时对高斯椭球进行类似传统图形学的变换,最后在变换后的空间中进行类似光栅化的操作,这被称为 forward mapping
而这两种方法都需要用到体渲染
体渲染主要是为了解决云、烟、果冻这类非刚性物体的渲染建模,为了建模这种非刚性物体的渲染,体渲染把气体等物质抽象成一团飘忽不定的粒子群。光线在穿过这类物体时,其实就是光子在跟粒子发生碰撞的过程
体积通常表示为微小的微分圆柱体,用 $L$ 来表示入射或出射光子数量,$L_i$ 表示入射光量,$L_o$ 表示出射光量。它其实就是 radiance
在一个粒子群中,光子与粒子发生的作用可以分为四种:
- 吸收(absorption):光子被粒子吸收
- 放射(emission):粒子本身释放光子
- 外散射(out-scattering):光子撞到粒子后可能弹射到其他方向
- 内散射(in-scattering):其他方向的光子被弹射到当前方向
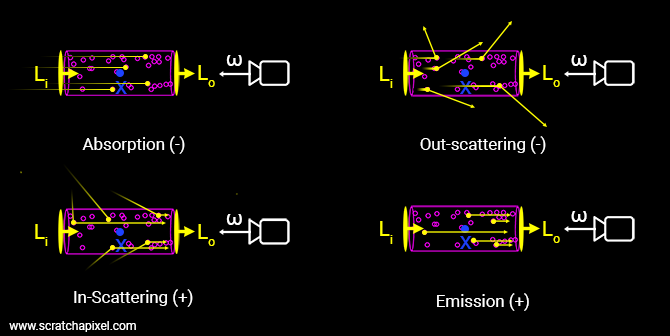
入射光与出射光之间的变化量由这四部分组成,即:
$$ \mathrm dL(x,\boldsymbol\omega) = \text{emission} + \text{in-scattering} - \text{out-scattering} - \text{absorption} $$其中,$\boldsymbol \omega$ 是摄像机朝向,由于光线从远处向摄像机发射,$x$ 表示当前位置距离粒子群入口的距离
吸收与吸收系数
在吸收部分,一个重要的参数是吸收系数 $\sigma_a$,它表示光在介质中传播每单位距离被吸收的概率密度,单位是距离的倒数
如果只考虑吸收,那么会有:
$$ \mathrm dL=-\sigma_aL(x,\boldsymbol\omega)\mathrm dx $$解这一个常微分方程可以得到:
$$ L(x,\boldsymbol\omega)=e^{-\sigma_ax}L(0,\boldsymbol\omega) $$这叫做比尔——朗伯定律
外散射与消光系数
外散射也有一个系数 $\sigma_s$ 叫做散射系数,与吸收系数基本相同,散射系数描述了光子在单位距离内被散射的概率,对内外散射相同
仍然可以写出一个相似的方程:
$$ \mathrm dL=-\sigma_sL(x,\boldsymbol\omega)\mathrm dx $$吸收和外散射部分加起来被称为消光系数,记作 $\sigma_t$,即:
$$ \sigma_t=\sigma_a+\sigma_s $$如果同时考虑吸收和外散射,那么有:
$$ \mathrm dL=-\sigma_tL(x,\boldsymbol\omega)\mathrm dx $$对于非均匀介质来说,消光系数(和散射系数)可能随位置不同而不同,即称为一个函数 $\sigma_t(x)$,此时可以写出一般形式的方程:
$$ \mathrm dL=-\sigma_t(x)L(x,\boldsymbol\omega)\mathrm dx $$解出来就是:
$$ L(x,\boldsymbol\omega)=e^{-\int_0^x \sigma_t(s)\mathrm ds}L(0,\boldsymbol\omega) $$内散射
碰上粒子的光子有概率向各个方向弹射,设与入口距离为 $x$,入射方向为 $\boldsymbol i$,出射方向为 $\boldsymbol o$,那么概率可以写成一个函数 $f_p(x,\boldsymbol i,\boldsymbol o)$
这叫做相位函数,它满足对称性,即 $f_p(x,\boldsymbol i,\boldsymbol o)=f_p(x,\boldsymbol o,\boldsymbol i)$
那么内散射对应的方程即:
$$ \mathrm dL=\sigma_s(x)\left[\int_{\mathbb S^2}f_p(x,\boldsymbol\gamma,-\boldsymbol\omega)L(x,\boldsymbol\gamma)\mathrm d\boldsymbol\gamma\right]\mathrm dx $$我们把右侧的积分记为 $L_s(x,\boldsymbol\omega)$,即:
$$ L_s(x,\boldsymbol\omega)=\int_{\mathbb S^2}f_p(x,\boldsymbol\gamma,-\boldsymbol\omega)L(x,\boldsymbol\gamma)\mathrm d\boldsymbol\gamma $$加上之前的吸收和外散射,方程就变成了:
$$ \frac{\mathrm dL}{\mathrm dx}=-\sigma_t(x)L(x,\boldsymbol\omega)+\sigma_s(x)L_s(x,\boldsymbol\omega) $$放射
放射部分仍然与 $\sigma_a$ 有关,参考 https://zhuanlan.zhihu.com/p/595117334
一般用 $\sigma_a$ 乘上一个 $L_e$ 表示放射部分,方程就变成了:
$$ \frac{\mathrm dL}{\mathrm dx}=-\sigma_t(x)L(x,\boldsymbol\omega)+\sigma_s(x)L_s(x,\boldsymbol\omega)+\sigma_a(x)L_e(x,\boldsymbol\omega) $$这是一个 $y'+p(x)y=q(x)$ 形式的微分方程,代入通解:
$$ y(x) = \left[\int_0^xq(t)e^{\int_0^tp(t')dt'} dt + C\right] e^{-\int_0^xp(t)dt} $$可以得到:
$$ L(x,\boldsymbol\omega)=\left[\int_0^x[\sigma_s(t)L_s(t,\boldsymbol\omega)+\sigma_a(t)L_e(t,\boldsymbol\omega)]e^{\int_0^t\sigma_t(t')\mathrm dt'}\mathrm dt+L(0,\boldsymbol\omega)\right]e^{-\int_0^x\sigma_t(t)\mathrm dt} $$这就是体渲染方程
3DGS 中的相机空间与射线空间
高斯椭球从世界空间(源空间)先变换到相机空间,然后再变换到射线空间
- 世界空间与相机空间与传统图形学中概念相似,这是一个仿射变换
- 从相机空间到射线空间的变换在传统图形学中类似投影变换,属于非仿射变换
相机空间与射线空间的概念与传统图形学有所不同
在相机空间中,一个点 $(x_0,x_1,x_2)^T$ 的各个坐标表示:
- $x_0$:水平偏移(左右)
- $x_1$:垂直偏移(上下)
- $x_2$:深度(距离相机沿光轴的方向)
在针孔摄像机模型中,所有射线都从相机中心 $\boldsymbol o$ 发出,然后穿过一个固定的平面,通常定义在 $z=f$ 处($f$ 为焦距),这叫做像平面
在这里情况相似,对于相机空间中的点 $(x_0,x_1,x_2)$,我们可以用一个二维坐标表示 $\boldsymbol o$ 到该点的射线方向:
$$ \hat{\boldsymbol x}=\left(\frac{x_0}{x_2},\frac{x_1}{x_2}\right)^T $$可以看成 $z=1$ 作为像平面,这样的话一个像素点 $(u, v)$ 就对应了相机发出的一条射线
我们可以将射线方向与该点与 $\boldsymbol o$ 的距离一起包起来,这唯一确定了三维空间中的一个点,这就是射线空间:
$$ \boldsymbol x=\left(\hat{\boldsymbol x},\Vert(x_0,x_1,x_2)^T\Vert\right)^T $$论文中的示意图:
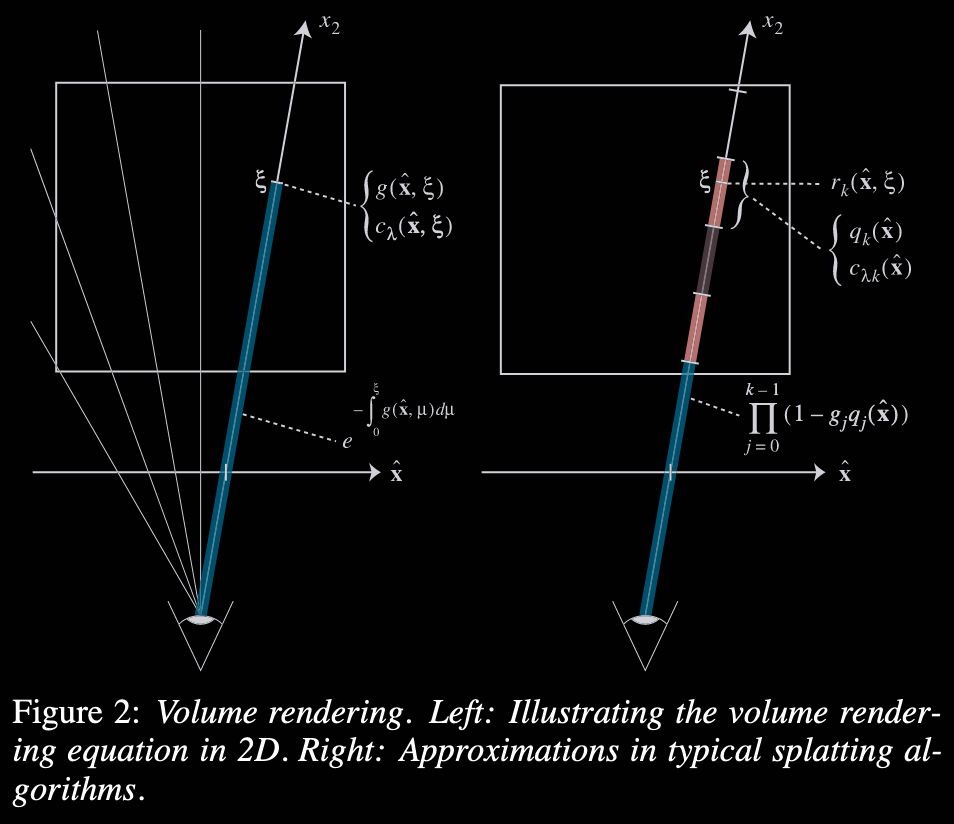
3DGS 中的体渲染方程
我们让 $L(0,\boldsymbol\omega)=0$,即将背景项设为 $0$,那么渲染方程就可以写成:
$$ L(x,\boldsymbol\omega)=\int_0^x[\sigma_s(t)L_s(t,\boldsymbol\omega)+\sigma_a(t)L_e(t,\boldsymbol\omega)]e^{-\int_t^x\sigma_t(t')\mathrm dt'}\mathrm dt $$我们令:
$$ S(x)=\sigma_s(x)L_s(x,\boldsymbol\omega)+\sigma_a(x)L_e(x,\boldsymbol\omega) $$那么原方程就可以写成:
$$ L(x,\boldsymbol\omega)=\int_0^xS(t)e^{-\int_t^x\sigma_t(t')\mathrm dt'}\mathrm dt $$由于上面的渲染方程采用的是从远到近的逻辑,而 3DGS 中采用由近及远的顺序,所以指数上换成 $-\int_0^t\mathrm dt'$
并且我们可以把 $S(x)$ 简化一下,认为它是 $\sigma_t$ 乘上某个东西,即:
$$ S(x)=\sigma_t(x)L_t(x,\boldsymbol\omega) $$那么渲染方程就可以写成:
$$ L(x,\boldsymbol\omega)=\int_0^x\sigma_t(t)L_t(t,\boldsymbol\omega)e^{-\int_0^t\sigma_t(t')\mathrm dt'}\mathrm dt $$和论文中的形式相同:
$$ \boxed{I_\lambda(\hat{\boldsymbol x})=\int_0^Lc_\lambda(\hat{\boldsymbol x},\xi)g(\hat{\boldsymbol x},\xi)e^{-\int_0^\xi g(\hat{\boldsymbol x},\mu)\mathrm d\mu}\mathrm d\xi} $$其中:
- $I_\lambda(\hat{\boldsymbol x})$ 表示投影平面中 $\hat{\boldsymbol x}$ 这个像素点的光强
- $c_\lambda(\hat{\boldsymbol x},\xi)$ 表示射线空间中 $(\hat{\boldsymbol x},\xi)$ 这个点粒子的颜色或 radiance,在 3DGS 中由 SH 系数决定
- $g(\hat{\boldsymbol x},\xi)$ 表示射线空间中 $(\hat{\boldsymbol x},\xi)$ 这个点的消光系数
- $e^{-\int_0^\xi g(\hat{\boldsymbol x},\mu)\mathrm d\mu}$ 可以理解成“能到达相机的概率”
- $\int_0^L\mathrm d\xi$ 表示从 $\boldsymbol o$ 开始一直积分到 $(\hat{\boldsymbol x},L)$ 处
也就是在射线空间中沿着 $\hat{\boldsymbol x}$ 表示的这条射线,在距离 $\xi$ 处,每一个粒子的 radiance 贡献,按其“能到达相机的概率” $e^{-\int_0^\xi g}$ 加权并累加
它在形式上退化成了无散射,仅放射/吸收的模型