3DGS 5. SFM 方法生成初始化点云

3DGS 的整体流程如下图所示：

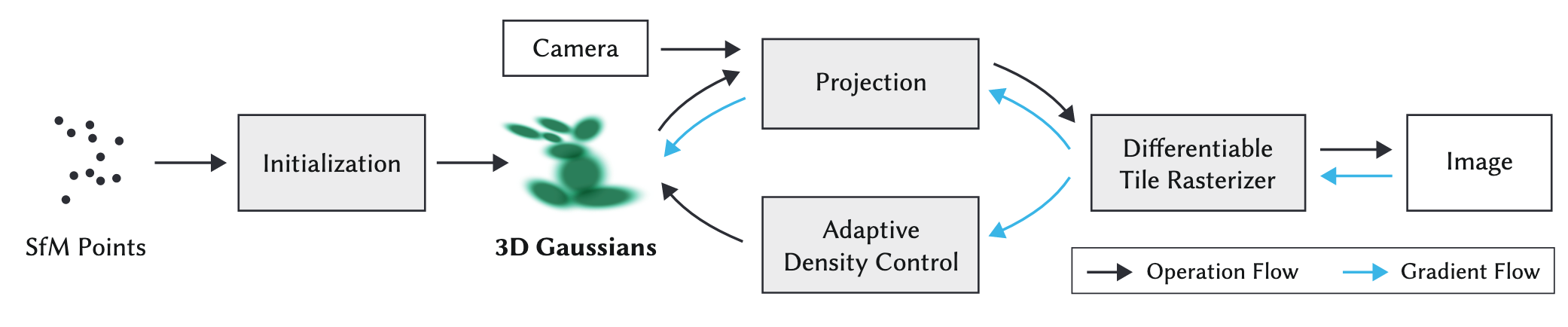
它非常依赖于 SFM 方法生成点云。SFM（structure-from-motion）算法是一种基于各种收集到的无序图片进行三维重建的离线算法。顾名思义是从运动中（不同时间拍摄的图片集）恢复物体的三维结构

针孔照相机模型与相机参数

针孔照相机模型是计算机视觉领域中主流的成像模型，可以简单地把它看作一个盒子，在盒子的某个面有一个小孔；

场景中的每一点都有一根光线穿过针孔（pinehole），交于相对的像平面（image plane）
它给定了一个透视投影（perspective projection），将三维空间映射到二维平面上
成像是翻转的，可以考虑针孔另一侧的虚拟像平面（virtual image plane）来纠正成像的翻转

示意图如下：

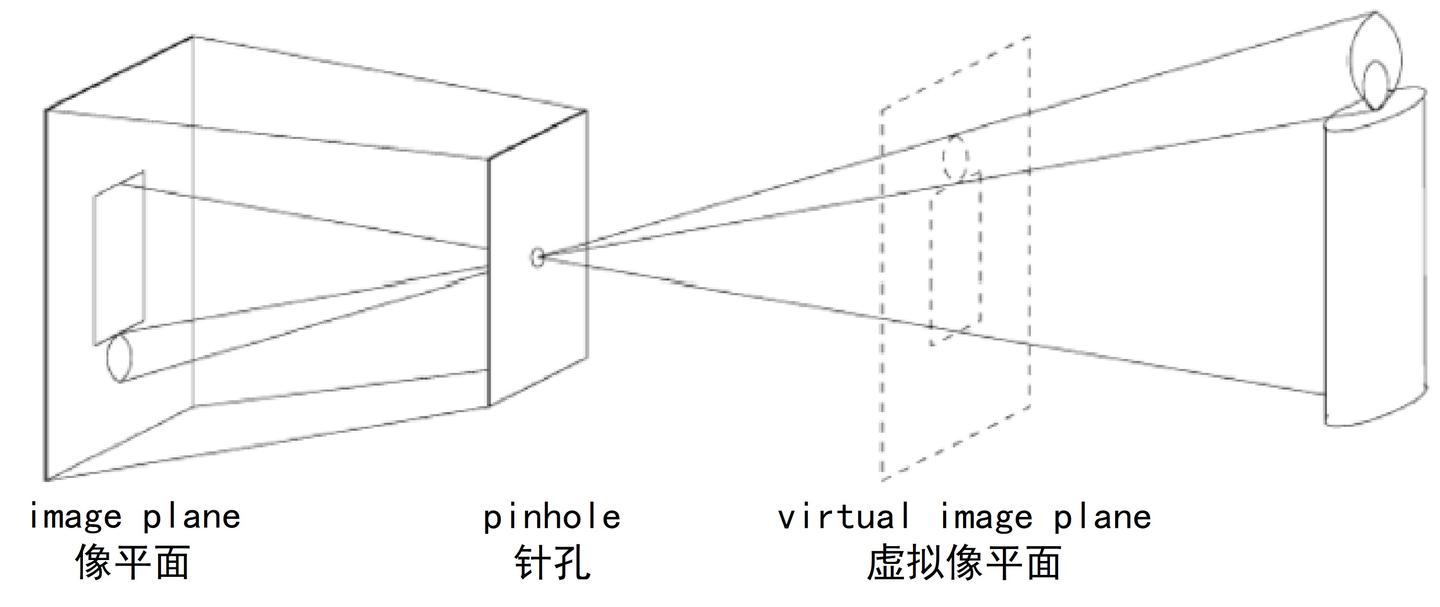
针孔照相机模型给定了从真实世界一点 $\boldsymbol p=(x,y,z,1)^T$ 到像平面上一点 $\boldsymbol q=(x',y',1)^T$ 的投影关系，而该关系可由如下公式所描述：

$$ \lambda\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix}=\begin{bmatrix} f_x & s & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix}\begin{bmatrix} \boldsymbol R & \boldsymbol T \\ \boldsymbol 0 & 1 \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} $$

等式右侧三个矩阵分别为：

相机内参 $\boldsymbol K$，由焦距（$f_x$ 与 $f_y$）、主点（横坐标 $c_x$，纵坐标 $c_y$）、轴间倾斜量（$s$）组成
规范化投影矩阵 $\boldsymbol\Pi_0$，用于将齐次坐标转换成三维坐标
相机外参 $\boldsymbol g$，由旋转分量与平移分量组成，表示相机的姿态

另外，$\lambda$ 表示等式右侧运算完后要除以 $z$ 坐标 $\lambda$

这个公式可以简写成：

$$ \lambda\boldsymbol q=\boldsymbol K[\boldsymbol R,\boldsymbol T]\boldsymbol p $$

相机外参比较好理解，内参这五个参数含义为：

焦距 $f_x$ 和 $f_y$ 其实是相机的焦距 $f$ 除以像素物理尺寸 $m_x$、$m_y$，表示像素尺度下的焦距
主点 $(c_x,c_y)^T$ 表示成像坐标原点相对于图像坐标的偏移，图像中心不一定是光轴穿过图像平面的点
轴间倾斜量 $s$ 一般为 $0$